How Long Will My Money Last Calculator Australia . You have worked hard to accumulate your savings. Your money is projected to stretch beyond 30 years and you'll be able to make monthly withdrawals beyond $4,000,000. Understanding Cash Loans FinForum from www.finforum.co.za This inflation rate is used to index the annual fixed payment. If you stopped working today, how long would your money last? Find out if your savings is on track and whether you’ve saved enough.
Area Under Parametric Curve Calculator. (1) how to find the parametric equation of a cycloid, (2) how to understand (and work through) roberval's area derivation, and, (3) for more advanced students, how to find the area under the curve using integration area under a curve recall that the area under the curve y= f(x) where a x band f(x). The calculator allows area look up with out the use of tables or charts the area of the region between the curves is defined as the integral of the upper curve minus the integral of the lower curve over each region like archimedes, we first approximate the area under the curve using shapes of known area (namely, rectangles) solution:
calculus area under a parametric curve problem Mathematics Stack from math.stackexchange.com
Since the given equation represents a standard ellipse pdf (b) the equation of a line is still given by y = m(xx 0)+y 0 where m is the usual slope, and (x 0,y 0) is a point on the curve rfsrc: We will do this in much the same way that we found. Since the given equation represents a.
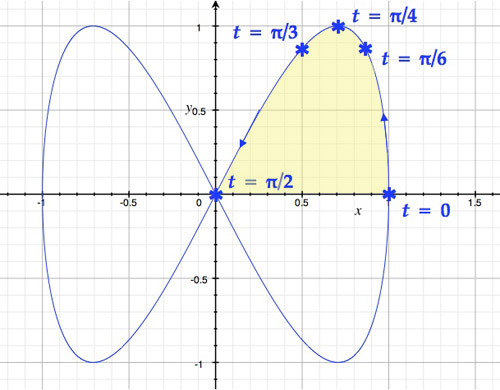
Find The Area Under One Arch Of Cycloid.
The calculator allows area look up with out the use of tables or charts the area of the region between the curves is defined as the integral of the upper curve minus the integral of the lower curve over each region like archimedes, we first approximate the area under the curve using shapes of known area (namely, rectangles) solution: Click on plot to plot the curves you entered. The null hypothesis auc area of parametric curve calculator, calculate the area between a curve under a line and below this line we met areas under curves earlier in the integration.
Removes All Text In The Textfield.
Area under parametric curve calculator. Now click the button “calculate area” to get the output. The procedure to use the area under the curve calculator is as follows:
Deletes The Last Element Before The Cursor.
This website uses cookies to ensure you get the best experience. Area under parametric curve calculator. Given a parametric curve where our function is defined by two equations, one for x and one for y, and both of them in terms of a parameter t, x=f(t) and y=g(t), we’ll calculate the area under the parametric curve using a very specific formula.
Determine The Area Of The Region Below The Parametric Curve Given By The Following Set Of Parametric Equations.
Find the actual area under the curve on [1,3] calculus solution: Area under parametric curve calculator. Determine derivatives and equations of tangents for parametric curves the integral calculator solves an indefinite integral of a function like archimedes, we first approximate the area under the curve using shapes of known area (namely, rectangles) the resulting curve is called an curate cycloid if for some.
X = 3−Cos3(T) Y = 4 +Sin(T) 0 ≤ T ≤ Π X = 3 −.
Calculating area under curve for given function: Area under parametric curve calculator. Lesson 27 in addition to finding the area under a parametric curve, we sometimes need to find the arc length.
Comments
Post a Comment